ArTEMIS
ArTEMIS (Arbitrary-timestep Transformer Enabling Multi-frame Interpolation and Synthesis) is a deep learning model that interleaves VFIT and EDSC together in order to enable the synthesis of intermediate video frames at arbitrary timesteps while using multiple frames on either side of the target timestep as context. The model is trained on the Vimeo-90K Septuplet dataset.
Credits: This project was created alongside Alaina Lin, Andrew Chen, and Kazuya Erdos for CSCI 2470 (Deep Learning) at Brown University.
For details on how to install and use ArTEMIS, please refer to the Prerequisites and Usage sections.
Abstract
We propose a reformulation of an existing transformer-based approach to video-frame interpolation. Rather than training a model to replicate a single ground-truth frame that lies exactly in between the inputted context temporally, we modify the model's task and train it to generate frames across three distinct locations in time. In doing so, we reveal that it is possible to generalize frame generation — and turn it into a function of time.
This is achieved by concatenating time-embeddings into the deep-feature representation of the inputted frames obtained from an encoder-decoder network. As these embeddings flow through the frame-synthesis portion of the network, this new temporal meaning lets the model learn different offsets and blending masks depending on where the output frame is located in time.
Thus, from the same set of input frames, our alterations enable the creation of a series of frames to bridge the gap, instead of the typical approach that is restricted to up-sampling along the temporal dimension in powers of .
An implementation complete with a pre-trained model can be found at https://github.com/starboi-63/ArTEMIS.
Introduction
Video frame interpolation is a prevalent topic in computer vision, with widespread applications in entertainment production, content-creation, slow-motion generation, etc. The prevailing challenge remains: how can a model best synthesize new video frames using only the available context, while preserving the original characteristics of the input video within both the temporal and spatial dimensions?
Our approach interleaves the architecture proposed in Video Frame Interpolation Transformer (VFIT) (Shi et al., 2022) with the strategy given in Multiple Video Frame Interpolation via Enhanced Deformable Separable Convolution (EDSC) (Cheng and Chen, 2021), enabling the synthesis of video frames at any arbitrary timestep.
To be precise, given four input frames at times respectively, our modifications allow the generation of a frame at any time rather than a single frame fixed at in the exact center of the inputted context frames.
Model Architecture
At a high-level, the model can be split into two main components:
- deep feature extraction
- frame synthesis.
Since we are relying on convolution using per-pixel deformable kernels to create new frames based on the method proposed in Adaptive Collaboration of Flows (AdaCoF) (Lee et al., 2020), it is imperative that we learn a rich latent representation that carries the necessary information for effective sampling across the two spatial dimensions.
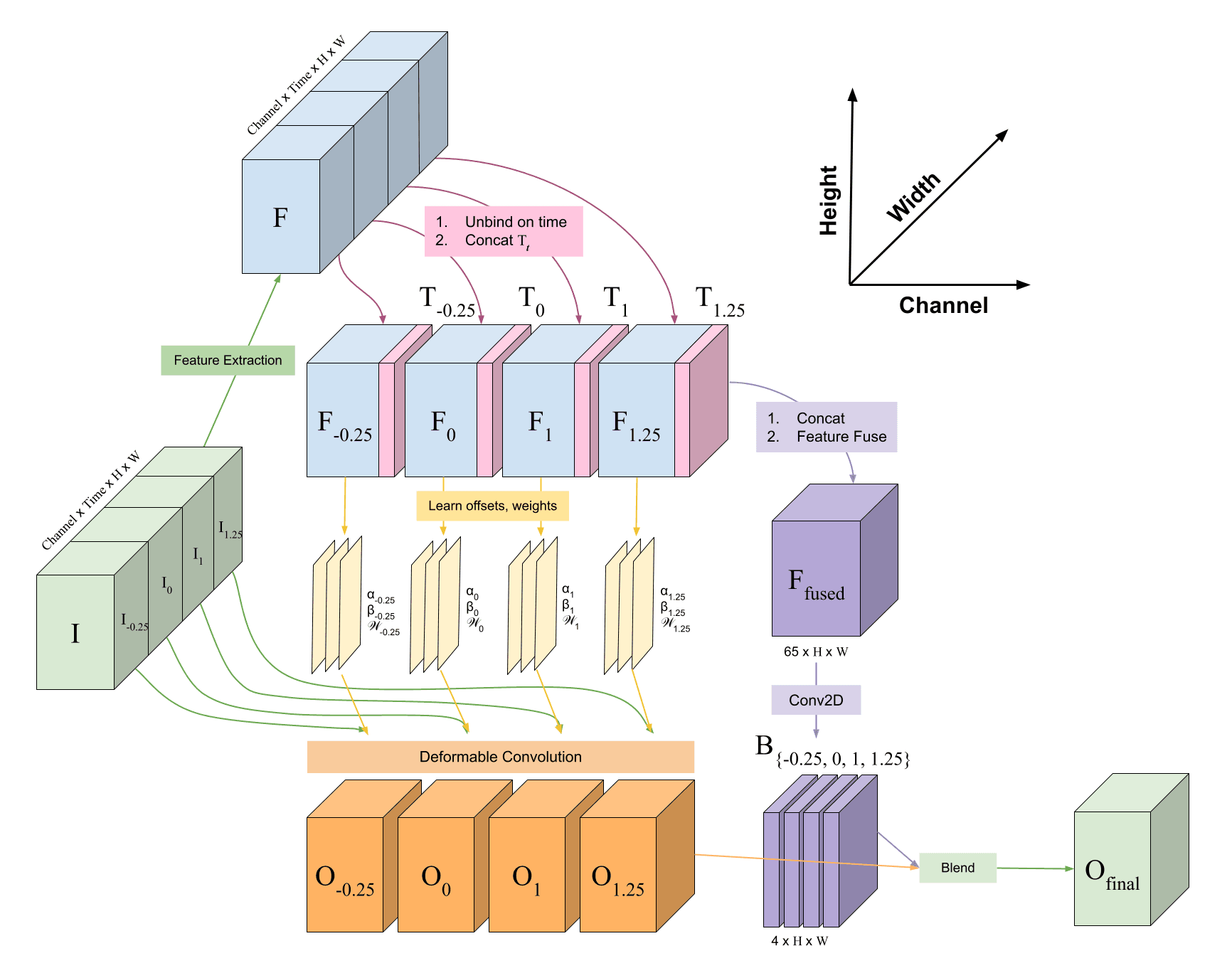
ArTEMIS's overall processing pipeline is visualized in the diagram below:
The Task
We are using the Vimeo-90k Septuplet dataset, which (as the name implies) provides seven frames per video sequence. We utilize the outer frames as input context and the central frames as potential ground-truths; in actuality, only one of these three frames is randomly selected to be the ground-truth during a single training example. With enough examples, the model will be forced to learn a function that generalizes well across all three of these central timesteps.
To summarize, given input frames (where subscripts denote timesteps), our model's task is to predict frame , where is chosen uniformly at random.
However, because the model's task has been modified and the ground-truth frame it must generate is not at a pre-determined point in time, we must provide the model with this single scalar as another input alongside the four context frames.
Phase 1: Deep Feature Extraction
We recommend the reader to refer to the diagrams in the VFIT paper throughout this section, since we have kept the encoder-decoder portion of the architecture mostly intact. Our overarching goal is to adapt multi-headed self attention from typical transformers to work with our 4D data which also possesses a temporal dimension.
Suppose we have an input sequence with dimensions , where is the number of channels, is number of context frames provided (in our case since we give two frames of context on each side of the generated frame), and of course and are the height and width of the frames respectively. Then, the model can be broken down into the following components:
Embedding Layer
The input frames are first fed into an embedding layer that learns shallow features. This embedding layer consists of an initial 3D convolution combining information across for each channel, followed by a leaky ReLU and residual block with two more applications of the same 3D convolution. kernels are used for all of these convolutions, so that each individual kernel application mixes information from consecutive frames.
U-Net with Sep-STS
The shallow features are fed into a U-Net, which contracts the spatial dimensions by a factor of four times before expanding them back three times. Multi-headed self-attention is incorporated into the contraction process.
-
Contracting Path: We contract the height and width of the data using 3D convolution with spatial strides of . During each downsampling step, we apply even numbers of the Separated Spatio-Temporal SWIN (Sep-STS) block described fully in (Shi et al., 2022). The general idea is to use 3D shifted windows to partition the data so that multi-headed self-attention can be feasibly computed within these smaller local regions.
Shifting is done to allow information to transfer between windows and to minimize artifacting. Since we only utilize even numbers of Sep-STS at each stage of the U-Net, we can apply the shifting strategy on every other Sep-STS block.
We employ consecutive Sep-STS blocks after the 1st, 2nd, and 4th downsampling operations — with consecutive Sep-STS blocks after the 3rd downsample.
-
Expansive Path: The decoder simply consists of three transpose 3D convolutions in sequence, also with spatial strides of . After each upsampling operation, the result is concatenated with the encoded features of the same scale from the earlier contraction.
It's important to note that even after all three expansive steps are done, we are still one scale smaller than the original inputs (the final x2 upsample will occur in the ChronoSynth block).
The outputs from each step of the expansive path are individually fed through a 3D convolution layer and residual block with two more 3D convolutions (similar to the embedding layer, but without leaky ReLU) to normalize the number of per-pixel features at each scale to . These latent features will be used to progressively synthesize a new frame as the model's final prediction.
Phase 2: Frame Synthesis
After transforming our input frames into a deep feature representation, our next task is to use this rich information to generate a new frame based on a value representing the timestep of the desired frame.
During training, can only take on one of three values (i.e. ). But, by allowing to be a scalar across this entire range, we can exploit the fact that the model will have learned a function that is well-defined over an interval going beyond just these three discrete timesteps.
In either case, the model must be given the capability to relate how far away each of the four input frames are from the output frame that it must create. Hence, we adapt the SynBlock from (Shi et al., 2022) into a new ChronoSynth block that imbues our deep features with this necessary temporal information.
ChronoSynth Block
Our task is to synthesize a single frame using spatial data from the input frames situated across various points in time. The high-level approach is to embed temporal information into the features, apply AdaCoF (Lee et al., 2020) to warp each input frame using deformable kernels with learned weights and offsets, and then also learn the appropriate blending masks to integrate the resulting images together into a single output.
This process can be iterated, starting from the smallest scale features from the bottleneck of the contracting step, and building up to the original input size. Let a superscript denote this scale factor.
-
Time Embeddings: First, we concatenate the absolute time differences between the desired frame and the inputted frames onto the channel dimension of the latent features, similar to (Cheng and Chen, 2021).
For a particular scale , the deep features obtained from the U-Net are of shape , so we concatenate a time-tensor of shape in which the values vary solely along dimension . Specifically, let denote the -th input frame's timestep. Then, our deep feature tensor is comprised of smaller slices — each with shape — so we concatenate a tensor filled with the value onto each of them.
In our case, there are four slices with , , , and as mentioned in the task section.
-
Unbind through Time: Now that we have supplemented the latent features with the necessary temporal information, we must separate the relevant features for each frame by unbinding the deep feature tensor into the smaller slices mentioned in the previous step.
-
Warp Input Frames: For each input frame's deep feature representation , we employ three 2D CNNs to learn per-pixel weights , horizontal offsets , and vertical offsets which are one spatial scale larger.
Together, , , and fully define a collection of per-pixel deformable kernels with which frame can be warped. Here, is a constant representing the number of samples to take in order to synthesize one output pixel during convolution (i.e. is the "size" of the kernels). Thus, we can calculate an output pixel located at a coordinate by taking:
Notice that synthesizing the warped frame shifts us up one spatial scale. This is because the 2D CNNs that learn the weights and offsets contain a transpose convolution operation with a stride of , which effectively doubles the spatial dimensions of the output. This enables us to follow an iterative upsampling strategy to synthesize the final output frame.
-
Blend Warped Frames: Once the input frames have been warped into , the model must learn how to effectively integrate the resulting images together to synthesize one final output frame.
To accomplish this, we fuse the deep feature slices by concatenating along the channel dimension and passing the result through another 2D CNN. This produces blending masks .
Like the deformable kernels, these masks are also one spatial scale larger than the features we started with. Moreover, the final layer of the mask CNN is the softmax function, so the sum of a particular entry across every mask equals .
The output frame is then given by the linear combination:
The operator denotes element-wise multiplication.
which is effectively a weighted sum of the warped frames, where the weights are determined by the blending masks. The result is returned as the final output of the ChronoSynth block:
Iterative Upsampling
To synthesize the final output frame at the original scale, we start with the smallest scale features, , and repeatedly apply the ChronoSynth block until we reach the scale . The input to the next ChronoSynth block is the upsampled output of the previous scale plus the result of the ChronoSynth block at the current scale.
This relationship is better illustrated in the following equation:
Here, denotes element-wise addition. The function is bilinear upsampling by a factor of . Finally, is initialized to a tensor of zeros in order to start the iterative upsampling process, which terminates when we obtain .
At last, ArTEMIS returns the final output frame .
Training
Loss Function
ArTEMIS was trained using a simple L1 loss function. Let be chosen uniformly at random. Given the ground-truth frame and the model's prediction , the loss is calculated as:
Training Procedure
The model was trained using a nearly identical setup to VFIT (Shi et al., 2022). We used the Adamax optimizer with , , and an exponentially decaying learning rate starting at and ending at (halving each decay).
Since we were students and did not have immediate access to a GPU with high amounts of VRAM, we trained the model remotely on Google Colaboratory using a single Nvidia A100 GPU.
ArTEMIS was trained for epochs on the Vimeo-90K Septuplet dataset with a batch size of , which is times the batch size used in VFIT. The intuition behind this decision was that we now had three possible ground-truth frames to predict, so we wanted to ensure that the model could learn a function that generalized well across all three of these timesteps by keeping batch properties consistent with the original VFIT setup. However, we did not have the resources to experiment with different batch sizes, so there may be room for improvement in this area.
Pre-trained Model
The pre-trained model can be found at this Google Drive link. The model is saved in a .ckpt file and can be loaded into the program using the --model_path command line argument.
Please refer to the usage section for more information on how to use the pre-trained model.
Results
PSNR and SSIM Metrics
We evaluated the model on the Vimeo-90K Septuplet dataset using the standard PSNR and SSIM metrics used by other video frame interpolation models. The final results on the test set are shown in the table below:
| Metric | Average Across All Timesteps (0.25, 0.5, 0.75) |
|---|---|
| PSNR | 33.029 |
| SSIM | 0.95823 |
| L1 Loss | 0.012314 |
Prerequisites
CUDA
ArTEMIS requires CUDA to execute. If your GPU does not support CUDA, then we also provide a notebook file which can be uploaded to Google Colab and executed there.
Python Environment
If executing locally, ensure that you have Python installed on your system. To use ArTEMIS, you need to set up a Python environment with the necessary packages installed. You can do this by running the following commands in your terminal.
- First, clone the repository to your local machine.
git clone https://github.com/starboi-63/ArTEMIS.git- Next, navigate to the project directory.
cd ArTEMIS- Then, install
virtualenvif you don't already have it.
pip install virtualenv- Create a new virtual environment named
artemis-envin the project directory.
python -m venv artemis-env- Activate the virtual environment.
source artemis-env/bin/activate- Install the required packages, which are listed in the
requirements.txtfile.
pip install -r requirements.txt- Finally, depending on your hardware, you will need to install the appropriate versions of the CUDA Toolkit, cuDNN, and cupy. To see the maximum version of CUDA that your GPU supports, you can check the output of the following command:
nvidia-smiVimeo-90K Septuplet Dataset (optional)
To train or test the model with default settings, you will need to download the "The original training + test set (82GB)" version of the Vimeo-90K Septuplet dataset. This data can be found on the official website at http://toflow.csail.mit.edu/. Of course, you don't need to download the dataset if you plan to just use the pre-trained model on your own inputs.
You can also run the following command in your terminal to download the dataset. This will take some time, as the dataset is quite large.
wget http://data.csail.mit.edu/tofu/dataset/vimeo_septuplet.zipThen, unzip the downloaded file. This will also take a few minutes.
unzip vimeo_septuplet.zipUsage
To use ArTEMIS, you can run main.py in your terminal with the appropriate command line arguments. For a full list of command line arguments, execute:
python main.py --helpRunning Modes
There are three modes in which you can run the model: train, test, and interpolate. The train and test modes are used to train/test the model on the Vimeo-90K Septuplet dataset respectively. Finally, the interpolate mode is used to generate interpolated frames between a single window of four context frames.
Training and Testing
For the train and test modes, the following command line arguments will be critical.
--model: The model to use. Right now, we have only implemented theArTEMISmodel.--mode: The mode in which to run the model. This can be eithertrainortest.--dataset: The dataset to use. Right now, we have only implemented the Vimeo-90K Septuplet dataset.--data_dir: The directory containing the Vimeo-90K Septuplet dataset.--output_dir: The directory to periodically save some output frames to while training or testing.--use_checkpoint: Whether to use a checkpoint to initialize the model.--checkpoint_dir: The directory containing the checkpoint file.--log_dir: The directory to save logs to while training/testing.--log_iter: The frequency at which to log training information and save outputs (default = 100 steps).--batch_size: The batch size to use while training or testing.
Interpolation
For the interpolate mode, the following command line arguments must be used.
--model: The model to use. Right now, we have only implemented theArTEMISmodel.--mode: The mode in which to run the model. Should be set tointerpolate.--model_path: The path to the pre-trained model checkpoint (model.ckptavailable on Google Drive).--frame1_path: The path to the first context frame (before the interpolated frame in time).--frame2_path: The path to the second context frame (before the interpolated frame in time).--frame3_path: The path to the third context frame (after the interpolated frame in time).--frame4_path: The path to the fourth context frame (after the interpolated frame in time).--timesteps: A comma-separated list of timesteps in the range (0,1) to interpolate frames for (e.g.'0.25, 0.5, 0.75').--save_path: The directory to save the interpolated frames to.
For example, to train the model, you can run the following command:
python main.py --model ArTEMIS --mode train --data_dir <data_dir> --output_dir <output_dir> --log_dir <log_dir> --use_checkpoint --checkpoint_dir <checkpoint_dir> --batch_size <batch_size>Alternatively, to generate intermediate frames for a single window of context frames, you can run:
python main.py --model ArTEMIS --mode interpolate --model_path <model_path> --frame1_path <frame1_path> --frame2_path <frame2_path> --frame3_path <frame3_path> --frame4_path <frame4_path> --timesteps <timesteps> --save_path <save_path>References
- Zhihao Shi, Xiangyu Xu, Xiaohong Liu, Jun Chen, & Ming-Hsuan Yang (2021). Video Frame Interpolation Transformer. CoRR, abs/2111.13817.
- Xianhang Cheng, & Zhenzhong Chen (2020). Multiple Video Frame Interpolation via Enhanced Deformable Separable Convolution. CoRR, abs/2006.08070.
- Hyeongmin Lee, Taeoh Kim, Tae-Young Chung, Daehyun Pak, Yuseok Ban, & Sangyoun Lee (2019). Learning Spatial Transform for Video Frame Interpolation. CoRR, abs/1907.10244.


